Využití Maxwellovy věty pro podrobnou diagnostiku stavu mostu

Článek je věnován aplikaci Maxwellovy věty o vzájemnosti přetvoření pro podrobnou diagnostiku globálního i lokálního stavu konstrukce při experimentálním vyšetřování. Popsaný postup je možno aplikovat zcela samostatně, lze jím ale také jednoduše a velmi efektivně doplnit zatěžovací zkoušky mostů při minimální spotřebě času a zanedbatelných nákladech navíc.

Maxwellova věta o vzájemnosti přetvoření a příčinkové čáry

Zjišťování skutečného stavu konstrukce je jednou ze základních činností, které se provádějí po dobu životnosti mostu. Jedná se o úkony spojené s uvedením mostu do provozu, jeho správou a údržbou, případnými opravami a rekonstrukcemi a nakonec i s rozhodnutím, zda most zbourat, nebo ještě prodloužit jeho životnost.

Významnou úlohu při ověřování skutečného stavu mostu mají i experimentální postupy založené na zkoušení konstrukcí in situ. Charakteristickým rysem těchto postupů je vyšetřování odezvy konstrukce na nepohyblivé zatížení (statické či dynamické) umístěné v určité konfiguraci v neměnné pozici na konstrukci. Odezva je přitom vyšetřována ve větším počtu míst na konstrukci (tj. jedna poloha zatížení – větší množství míst osazených snímači). Pokud se při těchto metodách zatížení na konstrukci přece jenom pohybuje (např. při vyšetřování hodnot dynamického součinitele při přejezdech zkušebních vozidel po mostě), zajímá nás odezva konstrukce pouze v místech osazených snímači, nikoli v zatěžovací trajektorii.

Rozsah vyšetřování stavu konstrukce je proto ve všech těchto případech dán (omezen) množstvím snímačů, které máme k dispozici. Principy fungující v mechanice tuhých a poddajných těles a prostředí nám však umožňují postupy, kdy postačí velmi malé množství snímačů (extrémně pouze jediný) ke zjištění odezvy konstrukce v rozsáhlých oblastech nosného systému, tj. například i v rozsahu celého mostního pole a sousedních polí apod. Aplikací těchto postupů můžeme také provádět velmi podrobnou lokální diagnostiku. Tyto principy jsou známy již velmi dlouho, ale jejich praktická aplikace při experimentálním vyšetřování konstrukcí byla umožněna až v poslední době díky rychlému rozvoji a miniaturizaci elektroniky a související výpočetní techniky.

K přiblížení těchto principů se musíme vrátit až do druhé poloviny 19. století, přesněji do roku 1872, kdy byla odvozena a formulována tzv. Bettiho věta o vzájemnosti virtuálních prací. Tato věta praví, že součet virtuálních prací jedné zatěžovací soustavy na posunutích vyvolaných druhou zatěžovací soustavou rovná se součtu virtuálních prací druhé zatěžovací soustavy na posunutích vyvolaných první zatěžovací soustavou. Od ­Bettiho věty je potom už jen malý krok k Max­wellově větě o vzájemnosti přetvoření, která je speciálním případem Bettiho věty, kdy se obě zatěžovací soustavy zmíněné v Bettiho větě omezí na jediné „jednotkové“ břemeno. V důsledku zmenšení počtu břemen v obou zatěžovacích soustavách „zmizí“ v rovnici pro Bettiho větu na obou stranách sumace a při „jednotkových“ břemenech přejde rovnost virtuálních prací (tj. součinu síly a dráhy) v rovnost přetvoření. Maxwellovu větu pak můžeme zjednodušeně formulovat takto: posun v prvním místě ve směru první síly vyvolaný „jednotkovým“ břemenem ve druhém místě se rovná posunu ve druhém místě ve směru druhé síly vyvolanému „jednotkovým“ břemenem v prvním místě.

Maxwellova věta sice zmiňuje „statické“ síly a posuny, ale matematicky lze odvodit, že je obecně platná pro všechny parametry přetvoření, a to jak v případech statického, tak i dynamického zatěžování. Platí tedy, že se týká nejenom vzájemnosti posunů, ale též vzájemnosti pootočení a také vzájemnosti pootočení ve vztahu k posunům atd. A právě tato skutečnost rozšiřuje dále naše pole působnosti při experimentálním vyšetřování konstrukcí.

Maxwellova věta velice úzce souvisí s příčinkovými čárami, které se používají ve statice pro vyšetřování účinků pohyblivého zatížení na nosnou soustavu. Z porovnání klasické definice příčinkových čar a Maxwellovy věty jasně vyplývá, že příčinkové čáry deformačních veličin lze definovat právě pomocí Maxwellovy věty. Pro průhyby tedy podle definice platí, že příčinkovou čarou průhybu v daném bodě konstrukce je ohybová čára zkoumaného nosného systému od zatížení „jednotkovým“ břemenem v tomto bodě. Principielně shodná definice platí i pro pootočení a „jednotkový“ moment. K tomu je třeba dodat, že definice platí jak pro soustavy staticky určité, tak i pro soustavy staticky neurčité.

Aplikace Maxwellovy věty pro praktické použití při experimentálním vyšetřování

Definice příčinkových čar pomocí Maxwellovy věty nám dávají značné možnosti při experimentálním vyšetřování reálných stavebních konstrukcí. Definice totiž „funguje“ obousměrně. Máme-li k dispozici z výsledků měření průběh přetvoření v řadě bodů (i) na konstrukci od zatížení „jednotkovým“ břemenem v daném místě (x), máme vlastně i příčinkovou čáru pro dané místo (x) s pořadnicemi v této řadě bodů (i). A opačně, máme-li k dispozici z výsledků měření příčinkovou čáru pro dané místo (x) s pořadnicemi v řadě bodů (i), známe vlastně i přetvoření v této řadě bodů (i) od zatížení „jednotkovým“ břemenem v daném místě (x). Oba postupy bude lépe ukázat na praktických jednoduchých příkladech.

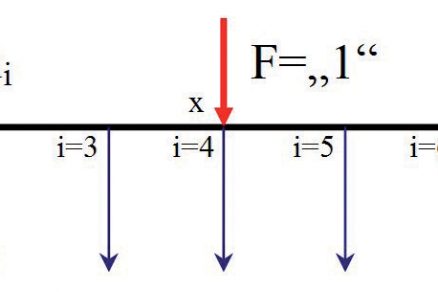
Obr. 1 Měření průhybů v místech „i“ při poloze břemene v místě „x“

Na obr. 1 máme statické schéma prostého nosníku, příp. výsek jednoho pole spojitého nosníku. Pokud podle tohoto schématu zatížíme reálnou konstrukci v místě (x) jednotkovým břemenem (např. 1 kN) a snímače průhybu umístíme např. do osmin rozpětí (i) (snímače = dolní šipky), dostaneme po spojení jednotlivých výsledků průběh průhybu po délce nosníku. Podle definice dle Max­wella je tato křivka současně příčinkovou čárou průhybu v místě (x).

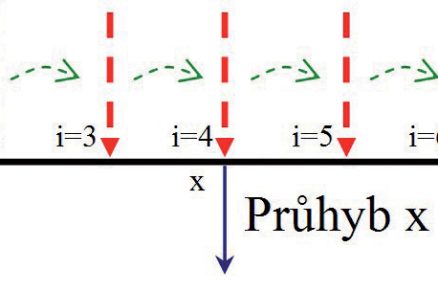
Tento postup je při reálném měření v terénu značně náročný na vybavení velkým počtem snímačů a na čas instalace. Můžeme tedy zkusit změřit pořadnice příčinkové čáry z hlediska měření „inverzním“ způsobem, tj. vyjít z podstaty konstrukce příčinkové čáry. To znamená, že nám postačí jediný snímač z předchozího případu a ten umístíme v bodě (x). Jednotkové břemeno (např. 1 kN) pak postupně přemísťujeme (podle obr. 2) po jednotlivých polohách (i), přičemž pro každou polohu břemene provedeme měření průhybu v bodě (x). Výsledky měření v bodě (x) pak vynášíme do odpovídajících poloh (i), při kterých bylo měření v bodě (x) provedeno.

Vynesené hodnoty průhybů v pozicích (i) jsou potom pořadnicemi příčinkové čáry průhybu v místě (x). Současně jsou ale podle Maxwella tyto pořadnice také pořadnicemi ohybové čáry nosníku v řadě bodů (i) pro zatížení jednotkovým břemenem v bodě (x). Opět jsme tedy, ale jiným způsobem, získali současně příčinkovou čáru a průběh průhybu po délce nosníku.

Obr. 2 Měření průhybů v místě „x“ postupně při polohách břemene v místech „i“

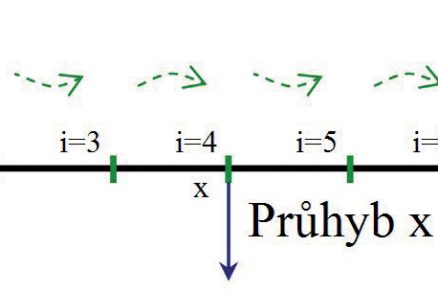
Tentokrát jsme ke výsledku dospěli již s jednoduchým měřicím vybavením, realizaci měření však komplikuje složitější organizace při přesunech zatížení. Možnosti, jak se dostat ke stejnému výsledku rychleji a jednodušeji, však ještě nejsou vyčerpány. Inspiraci můžeme najít u jednoho z typů dynamických zkoušek, kdy je konstrukce zatěžována přejezdy zkušebních vozidel předepsanými postupně zvyšovanými rovnoměrnými rychlostmi. Jednotlivé polohy zatížení z předchozího případu (obr. 2) můžeme tedy zkusit nahradit „jednotkovým“ pohyblivým zatížením podle obr. 3.

Obr. 3 Měření průhybů v místě „x“ při zatížení pohyblivým „jednotkovým“ zatížením

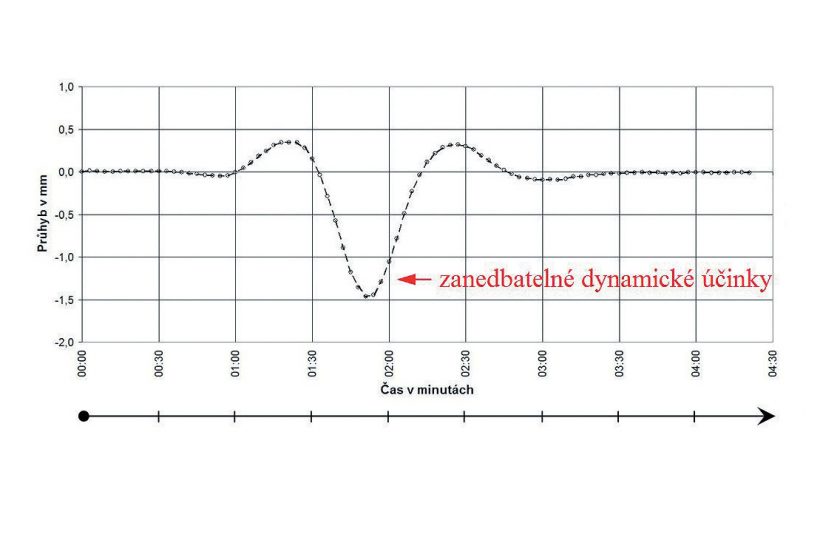
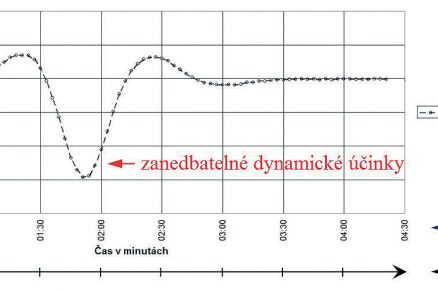
Pokud pro náš případ použijeme pohy­blivé zatížení, jehož rychlost nepřesahuje ­5 km/hod., lze toto zatížení považovat za statické, neboť dynamická složka je zanedbatelná. Měříme-li statickou odezvu od pohyblivého zatížení v konkrétním měřicím bodě (x) spojitě nebo s dostatečnou hustotou vzorkování (vyjádřenou např. časem přejezdu mezi jednotlivými body (i)), dostaneme jako výsledek časový záznam odezvy v daném měřicím bodě (x) (svislá osa: hodnota měřené veličiny/ průhybu, vodorovná osa: čas; viz obr. 4). Pokud je ovšem rychlost pohybu zatížení konstantní (v = konst.), lze nahradit čas (t) na vodorovné ose dráhou (s(t) = v . t). Když se podíváme na výstup po této transformaci, je zřejmé, že máme k dispozici příčinkovou čáru v bodě (x) a podle Maxwella též ohybovou čáru pro zatížení použitým břemenem v místě (x).

Obr. 4 Časový záznam odezvy na pohyblivé zatížení při konkrétním měření průhybů

Pořadnice příčinkové/ohybové čáry máme při tomto postupu vyčísleny v místech (i), která odpovídají použitému vzorkování, tj. v poloze pohyblivého zatížení na konstrukci v okamžicích automatických odečtů měřicího počítače. Pokud místo záznamu ve statickém módu použijeme program měřicího počítače pro dynamická měření, může být vzorkování velmi husté (řádově v milisekundách) a odezva je potom prakticky spojitá, tj. příčinkovou/ohybovou čáru máme též vyčíslenu téměř spojitě.
Zhodnotíme-li poslední popsaný postup, je zřejmé, že je velmi jednoduchý, rychlý a nenáročný na vybavení.

Při měření v terénu však musíme vzít v úvahu i řadu okolností, které snižují přesnost dosažených výsledků a s tím je třeba počítat (rozbor by vydal na další článek). Na druhou stranu se nám široce rozevírá paleta možností pro vyhodnocení výsledků měření, kdy můžeme přiměřeně využít metodiku hodnocení stavu konstrukce vyvinutou pro dynamické zatěžovací zkoušky. Po zkušenostech z celé řady experimentálních měření na různých typech konstrukcí s různými poruchami výše popsanou metodu velmi doporučujeme.

TEXT: Ing. Martin Krejcar, CSc.
OBRÁZKY: INSET s.r.o.

Martin Krejcar působí ve společnosti INSET s.r.o.

Článek byl uveřejněn v časopisu Inžinierske stavby/Inženýrské stavby.