Analýza fyzikálních vlastností stěny s aktivní tepelnou ochranou

Tento článek pojednává o způsobu šíření tepla, o akumulační schopnosti a o optimalizaci příslušné tloušťky tepelné izolace a rozestupu trubek v tomto typu stavebně-energetického systému. Článek pojednává též o přípravě experimentálních měření na fragmentu stěny s ATO v laboratorních podmínkách (Klimatická komora).

O stavebně-energetických systémech s aktivní tepelnou ochranou (ATO) víme zatím jen dost málo. Většina těchto systémů je ve fázi experimentálního ověření. Rozhodnutí pro tento výzkum vyplývá z možnosti aplikace ATO na bytové domy s železobetonovými obvodovými stěnami, které by mohly představovat dobrou akumulační schopnost. ATO by v tomto případě mohla plnit nejen funkci tepelné bariéry, ale i systému pro nízkoteplotní vytápění a vysokoteplotní chlazení [1].

Matematicko-fyzikální model

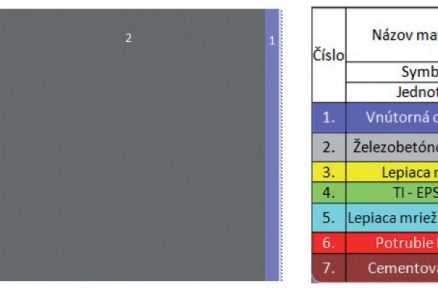
Jako základ pro simulace byl vyhotoven matematicko-fyzikální model (obr. 1 – legendy obrázků jsou ponechány v původním znění – pozn. red.). Simulace byly vykonávány v programu CalA (Calculation Area). Na obr. 1 (matematicko-fyzikální model) je vidět barevně odlišené materiály, z nichž se charakteristický fragment železobetonové stěny s aktivní tepelnou ochranou (ATO) skládá.

Obr. 1 Matematicko-fyzikální model fragmentu železobetonové stěny s ATO a jednotlivé materiálové charakteristiky podle STN 73 0540 – 3 podle[2].

 Jednotlivým materiálům byly v programu CalA přiřazeny materiálové charakteristiky:
d – tloušťka [m],
ρ – objemová hmotnost [kg/m³],
λ – součinitel tepelné vodivosti [W/m . K],
c – měrná tepelná kapacita [J/kg . K] [2].

Princip stacionárních a nestacionárních simulací v programu CalA

Pro stacionární (časově ustálený děj) platí:
1) Fourierova rovnice: q = A . U. Δθ,

kde    q je tepelný tok [W/m²],
    A – plocha [m²],
    U – součinitel prostupu tepla [W/m² . K],
    Δθ – rozdíl teplot [K];

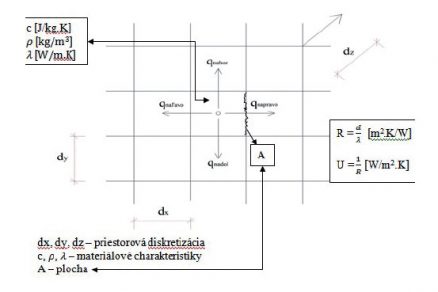
2) zákon zachování energie:
q_nahor + q_nadol + q_napravo + q_nalevo = 0   (Obr. 2)

Obr. 2  Grafické znázornění prostorové diskretizace sítě v programu CalA [3].

Pro nestacionární simulace (časově neustálený děj) platí rovnice:
Q = (m.c.Δθ)≥Q = (ρ.V.c.Δθ) [W], [J/s]

kde Q je tepelná energie [W],[J/s],
    ρ – objemová hmotnost [Kg/m³],
    c – měrná tepelná kapacita [J/kg . K],
    Δθ – rozdíl teplot [K], 273,15 K = 0 °C.

U nestacionárních simulací se setkáváme s poj­my jako „Time step” (časový krok) a „Time span” (délka časového kroku) a s pojmem „prostorová diskretizace” (V) – dx, dy, dz [3].

Parametrické stacionární simulace

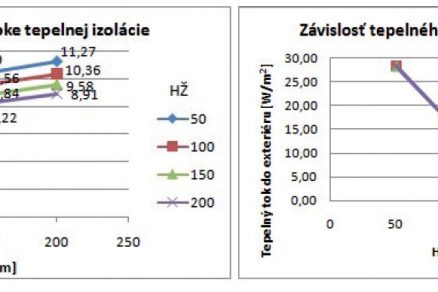
Předmětem parametrických simulací bylo zjistit vliv tloušťky tepelné izolace, vliv tloušťky železobetonu a vliv rozestupu potrubí na tepelný tok do exteriéru a do interiéru. Byly stanoveny okrajové podmínky: výpočtová teplota exteriérová teplota θ_e = –11 °C, teplota interiéru θ_i = 20 °C, teplota teplonosné látky θ_p = 25 °C a rozestup trubek L = 200 mm. Na obr. 3 jsou znázorněny křivky, které jsou barevně odlišeny podle měnící se tloušťky železobetonu. Například fialová křivka představuje 200mm tloušťku železobetonu. Z obr. 3  na levé straně je zřejmé, že se zvyšující se tloušťkou tepelné izolace tepelný tok směrem do interiéru roste a z obr. 3 na pravé straně je zřejmé, že naopak čím větší je tloušťka tepelné izolace, tím menší je tepelný tok do exteriéru, a též je vidět, že tloušťka železobetonu nemá téměř žádný vliv na tepelný tok směrem do exteriéru.

Obr. 3  Grafy znázorňující vliv tloušťky tepelné izolace na tepelný tok [2].

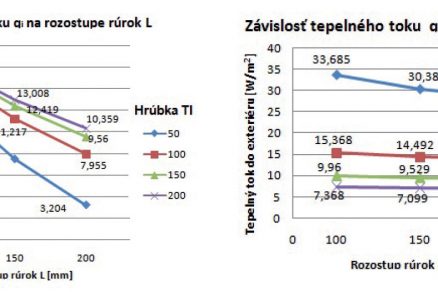
Dalším parametrem jako předmět zkoumání byl vliv rozestupu potrubí na tepelný tok. Fragment měl tloušťku železobetonu 100 mm. Měnila se tloušťka tepelné izolace, což je vidět barevně odlišenými křivkami z obr. 4. Měnil se také rozestup potrubí L [mm]. Byly stanoveny následující okrajové podmínky: výpočtová teplota exteriérová teplota θ_e = –11 °C, teplota interiéru θ_i = 20 °C, teplota teplonosné látky θ_p = 25 °C. Z obr. 4 vlevo je evidentní, že vliv rozestupu potrubí na tepelný tok směrem do interiéru je markantní. Se snižujícím se rozestupem potrubí tepelný tok směrem do interiéru roste a naopak. Z obr. 4 vpravo je zjevné, že vliv potrubí na tepelný tok směrem do exteriéru není až tak viditelný.

Obr. 4  Grafy znázorňující vliv rozestupu potrubí na tepelný tok [2].

Nestacionární simulace akumulace tepla fragmentu stěny s ATO

Předmětem zkoumání byly čtyři dny rozdělené po hodinách, přičemž okrajové podmínky byly stanoveny: výpočtová teplota exterié­rová teplota θ_e = –11 °C, teplota interiéru θ_i = 20 °C, teplota teplonosné látky θ_p = 25 °C. Parametry fragmentu byly následující: rozestup trubek L = 150 mm, tepelná izolace (TI) 150 mm a tloušťka železobetonu (ŽB) byla 100 mm. Systém ATO při 25 °C byl zapnut v čase 5:15 prvního dne a vypnut v čase 24:00 prvního dne. Sledovány byly teploty [K] v šesti bodech fragmentu. Na obr. 5 vidíme porovnání teplotního pole fragmentu s ATO a bez ATO.
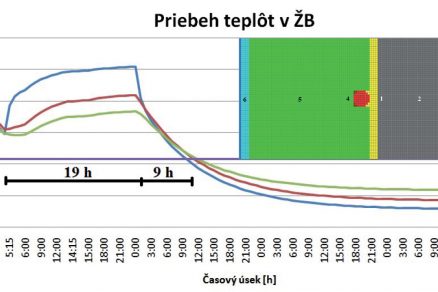
Z obr. 6 můžeme vypozorovat, že k tomu, aby se systém ustálil od doby zapnutí systému a vykazoval v bodě 1 teplotu 25 °C, je potřebných zhruba 19 h za daných okrajových podmínek. Doba chladnutí železobetonové stěny představuje asi 9 h [4].

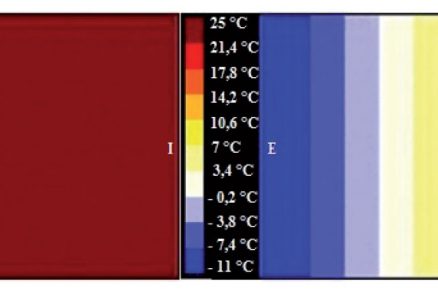
Obr. 5  Porovnání teplotního pole – zleva fragment s ATO, vpravo fragment bez ATO v čase 24:00 prvního dne [2], [4].

Obr. 6  Průběh teplot v železobetonu během čtyř dnů v bodě 1, 2 a 3 [2], [4].

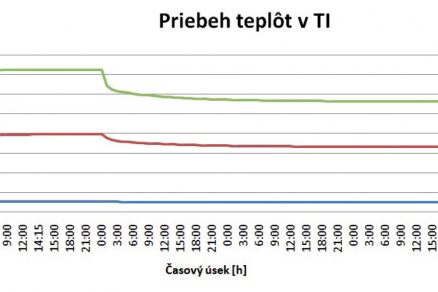
Obr. 7  Průběh teplot v tepelné izolaci fragmentu během čtyř dnů v bodě 4, 5 a 6 [2], [4].

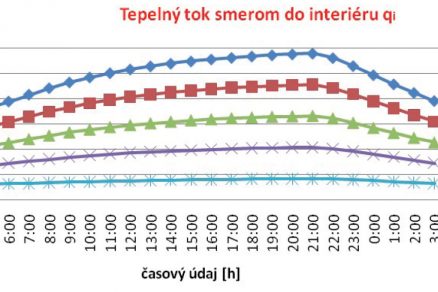
Obr. 8  Tepelný tok směrem do interiéru qi fragmentu během sedmi dnů v zimním období [2].

Následující nestacionární simulací byla simulace po sedm dnů v zimním období s parametry fragmentu: ŽB 100 mm, TI 150 mm, L 150 mm při okrajových podmínkách: θ_i = 20 °C, θ_e = od 0 °C po –14 °C. Bylo sledovaných pět oblastí fragmentu. Systém ATO byl vypínán vždy ve 22:00 hodin a zapínán vždy v 5:00. Teplota ATO se měnila z 20 °C na 25, 30, 35 a 40 °C. Z grafu na obr. 8 je evidentní, že při vypnutí systému ve 22:00 postupně tepelný tok qi klesá a naopak v čase 5:00 po opětovném spuštění systému ATO tepelný tok qi znovu roste. Markantní je i rozdíl tepelných toků qi při různých teplotách ATO. Na grafu na obr. 9 je vidět průběh tepelných toků qe při jednotlivých teplotách ATO. Z grafu na obr. 10 můžeme vypozorovat povrchové teploty při různých teplotách ATO a při různých teplotách θ_e , což můžeme vidět na obr. 11. Z obrázků 10 a 11 vidíme, že při teplotě ATO 20 °C jsou interiérové povrchové teploty pod 20 °C, kdežto při teplotách ATO 25, 30, 35 a 40 °C je interiérová povrchová teplota nad 20 °C. Dá se tedy říci, že při vyšší teplotě než 20 °C v ATO interiér vytápíme.

Porovnání ATO jako nízkoteplotní vytápění a ATO jako tepelná bariéra

Na obr. 12 vidíme porovnání teplotního pole a tepelných toků ATO při 25 °C, kde vidíme toky směřující do interiéru, což je potvrzeno i šipkami směrem doprava, naopak při ATO 20 °C směřují šipky vlevo směrem do exte­riéru i v železobetonové stěně.

Obr. 9  Tepelný tok směrem do exteriéru qe fragmentu během sedmi dnů v zimním období [2].

Obr. 10  Tepelný tok směrem do interiéru θ_pi fragmentu během sedmi dnů v zimním období [2].

Příprava na experimentální měření v laboratorních podmínkách

Byl vybetonován fragment železobetonové stěny o rozměrech 1140 × 1360 mm, který vidíme na obr. 8, kde lze také vidět systém technických zařízení budov zabezpečující ohřev a chlazení vody: 1 – elektrický ohřívač, 2 – zásobník vody, 3 – železobetonový fragment tloušťky 100 mm, 4 – skříňka pro měření a regulaci, 5 – oběhové čerpadlo, 6 – trojcestný ventil se servopohonem, 7 – přívod vody, 8 – odpadní potrubí, 9 – solenoid, 10 – průtokoměr, 11, 12 – snímače teploty na přívodním a vratném potrubí.

Obr. 11  Interiérová povrchová teplota θ_pi fragmentu během sedmi dnů v zimním období [2].

Obr. 12  Porovnání zleva ATO jako nízkoteplotní vytápění a ATO jako tepelná bariéra [2].

Regulace teploty ve zdroji tepla

V elektrickém ohřívači je umístěn odporový snímač teploty T5, který vysílá signál do regulátoru. V regulátoru se signál vyhodnotí a po dosažení nastavené žádané teploty regulátor přeruší přívod elektrického proudu do ohřívače, čímž se vypne z provozu. Regulátor opět obnoví přívod elektrické energie do ohřívače, až když teplota v ohřívači klesne pod nastavenou spínací diferenci. Na obr. 14c je vidět termovizní snímek fragmentu s teplotou teplonosné látky 40 °C na přívodním potrubí vytápěcího registru.

Obr. 13  Porovnání zleva ATO jako nízkoteplotní vytápění a ATO jako tepelná bariéra [2].

Regulace teploty vytápěcí a chladicí vody

Odporový snímač teploty T1, který je umístěn na přívodním potrubí za oběhovým čerpadlem, vysílá signál do regulátoru. V regulátoru je signál vyhodnocen a po překročení teploty nad žádanou hodnotu, regulátor vyšle signál do servopohonu trojcestného směsného ventilu. Servopohon spojitě otevírá přímou cestu ventilu a přimíchává vratnou vodu v takovém poměru, aby teplota přívodní vody měla vždy požadovanou hodnotu.

Regulace teploty a hlídání hladiny chladicí vody ve zdroji chladu

Ve spodní části zásobníku je umístěn odporový snímač teploty T3, který vysílá signál do regulátoru. V regulátoru je signál vyhodnocen a po překročení nastavené žádané teploty regulátor vyšle signál do elektromagnetického ventilu, který se otevře a začne se do zásobníku přimíchávat studená voda (přebytečná voda odtéká samospádem do kanalizace). Regulátor opět zavře elektromagnetický ventil, když teplota ve spodní části zásobníku klesne pod nastavenou spínací diferenci. Ve vrchní části zásobníku je umístěn snímač zaplavení. Po dosažení maximální hladiny vody v zásobníku snímač vyšle signál do regulátoru, který uzavře elektromagnetický ventil a zastaví tak přívod vody do zásobníku. Regulátor opět otevře elektromagnetický ventil, když hladina vody v zásobníku klesne pod maximální hodnotu.

Obr. 14  Systém TZB s fragmentem stěny a termovizní snímky s potrubním registrem

Závěr

Vzhledem k výsledkům stacionárních parametrických simulací, z nichž je zřejmé, že tloušťka železobetonové stěny nemá téměř žádný vliv na tepelný tok směrem do interiéru ani do exteriéru, byl stanoven optimální parametr tloušťky železobetonové stěny i s ohledem na omezené možnosti v klima-komoře na 100 mm. Výsledkem parametrických stacionárních simulací bylo i to, že tloušťka tepelné izolace má výrazný vliv na tepelné toky. Avšak optimální parametr tloušťky tepelné izolace byl stanoven na 100 mm. Optimální parametr rozestupu potrubí byl stanoven na 150 mm. Výsledkem první nestacionární simulace bylo zjištění doby náběhu (čas ustálení) systému ATO po zapnutí, a to konkrétně 19 h. Výsledkem je také zjištění doby vybíjení nahřáté stěny, respektive akumulační schopnosti ATO, a to konkrétně kolem 9 hodin. V druhé nestacionární simulaci můžeme za výsledek pokládat zjištění, že při daných okrajových podmínkách i po vypnutí systému ATO v době od 22:00 do 5:00 (využití tak nočního útlumu) dokážeme interiérový prostor vytápět, kromě případu, kdy v ATO využijeme teplotu 20 °C. Při teplotě 20 °C v ATO je tepelný tok směrem do interiéru opačný, což je vidět na obr. 10.
Výzkum bude pokračovat v laboratorních podmínkách v klima-komoře, kde se budou uskutečňovat měření na fragmentu železobetonové stěny s ATO v kooperaci se systémem, který je možné vidět na obr. 13 a o němž je více informací uvedeno v kapitole 7.

Poděkování patří firmě PAVJAN, s. r. o., za výrobu železobetonového fragmentu stěny a firmě Regulaterm, s. r. o., za výrobu TZB systému na vytápění a chlazení.

Obrázky: autor

Literatura
[1]    Kalús D. – Osvedčenie: Tepelnoizolačný panel pre systémy s aktívnym riadením prechodu tepla, 63 s. – SK 5725 Y1.
[2]    Šikula O. – Manuál k softwaru CalA (Calculation Area), Brno, ČR, 43 s., vydal Tribun EU, s. r. o., ISBN 978-80-7399-879-0.
[3]    Šikula O. – Počítačové modelování tepelně aktivovaných konstrukcí. Brno, ČR, 39 s.,
ISBN 978-80-214-4308-2.
[4]    Gebauer G. – Termika pro TZB – základní úlohy v příkladech. Vysoké učení technické v Brně, ČR 1996, 56 s., ISBN: 802140745X.

Ing. Martin Šimko
Autor je studentem doktorandského studia oboru Teorie a technika prostředí budov, Stavební fakulta STU v Bratislavě.

Článek byl uveřejněn v časopisu TZB HAUSTECHNIK.